Goal
정렬 알고리즘 중 Quick Sort 에 대해 알기
Quick Sort의 장· 단점
시간 복잡도 이해하기
자바로 구현할 줄 알기
Quick Sort (퀵 정렬) 알고리즘
★분할 정복(divide and conquer) 방법
작은 2개의 문제로 분리하고, 각각을 해결한 후, 결과를 다시 모아 원래의 문제를 해결한다.
설명
- 리스트 안에 한 요소를 선택 - 선택한 요소를 피벗(pivot)이라고 한다.
- pivot을 기준으로 작거나 큰 요소의 위치를 옮긴다.
- pivot 기준으로 왼쪽 : pivot 보다 작은 요소
- pivot 기준으로 오른쪽 : pivot 보다 큰 요소
- pivot을 제외한 왼쪽 list와 오른쪽 list를 재 정렬한다.
- 분할한 부분 리스트(왼쪽, 오른쪽) 에 대해 다시 pivot을 정한다.
- 2개의 부분 리스트로 나누는 과정을 반복한다.
- 더 이상 분할이 불가능 할때까지 (배열의 크기가 1일 때까지) 반복한다.
- 구체적 용어 설명
- 분할(Divide) : pivot을 기준으로 2개의 배열로 분할한다.
- 정복(Conquer) :
- 부분 배열을 정렬한다.
- 순환 호출을 이용해서 분할 정복을 반복한다.
- 결합(Combine) : 정렬된 부분 배열을 합친다.
STEP 1 - pivot 선정
- pivot 값 설정 (pivot값 설정 방식에 따라 수행시간의 차이가 난다.)
- 맨 왼쪽 값
- 가운데 값 (array size / 2)
- 맨 오른쪽 값
- 효율적인 pivot 선택 하는 방법 (median of three)
- 중간 크기의 숫자를 pivot으로 선정하는 것이 가장 효율적이다.
- 세 값 (처음, 가운데, 끝) 중 중간 값을 pivot으로 선정한다.
- 나머지는 일반 quick과 같다.
- 맨 왼쪽 값이나 오른쪽값을 pivot으로 선택할 경우
- 부분리스트를 나눌때 pivot값을 제외하고 나눌 수 있다.
- 그러나 가운데에 위치한 값을 pivot으로 선택한 경우
- 다양한 변수들로 인해 pivot값을 포함하고 나누게 된다.
- (이 부분 조사에 있어 시간이 오래걸렸다. 혹시나 틀렸다면, 댓글로 저에게 올바른 지식을 알려주세요.)
- 이 포스트에서는 가운데 값을 pivot 으로 선정해 보려고 한다.
- 예시 array [5, 8, 10, 6, 1, 3]
- 6(array size) / 2 = 3 -> pivot = 10
STEP 2
- 알아야 할 조건
- left는 pivot < left 일 때까지 우측으로 이동
- right는 pivot > right 일 때까지 좌측으로 이동
- 왼쪽(노랑)값이 pivot 값 보다 작은지 확인한다.
- 작다면 왼쪽에서 오른쪽으로 이동하면서 이를 반복한다.
- 왼쪽(노랑)값이 pivot 값 보다 크다면 오른쪽 값(파랑) 을 본다.
- 오른쪽(파랑)값이 pivot 값 보다 큰지 확인한다
- 크다면 오른쪽에서 왼쪽으로 이동하면서 이를 반복한다.
- 오른쪽(파랑)값이 pivot보다 작다면
- 왼쪽(노랑)값과 오른쪽(파랑)값을 SWAP한다.
- 왼쪽(노랑)과 오른쪽(파랑)이 만날때 까지 반복한다.
- 또는 오른쪽(파랑)이 왼쪽(노랑)을 교차해서 right> left 될 때 까지 반복한다.
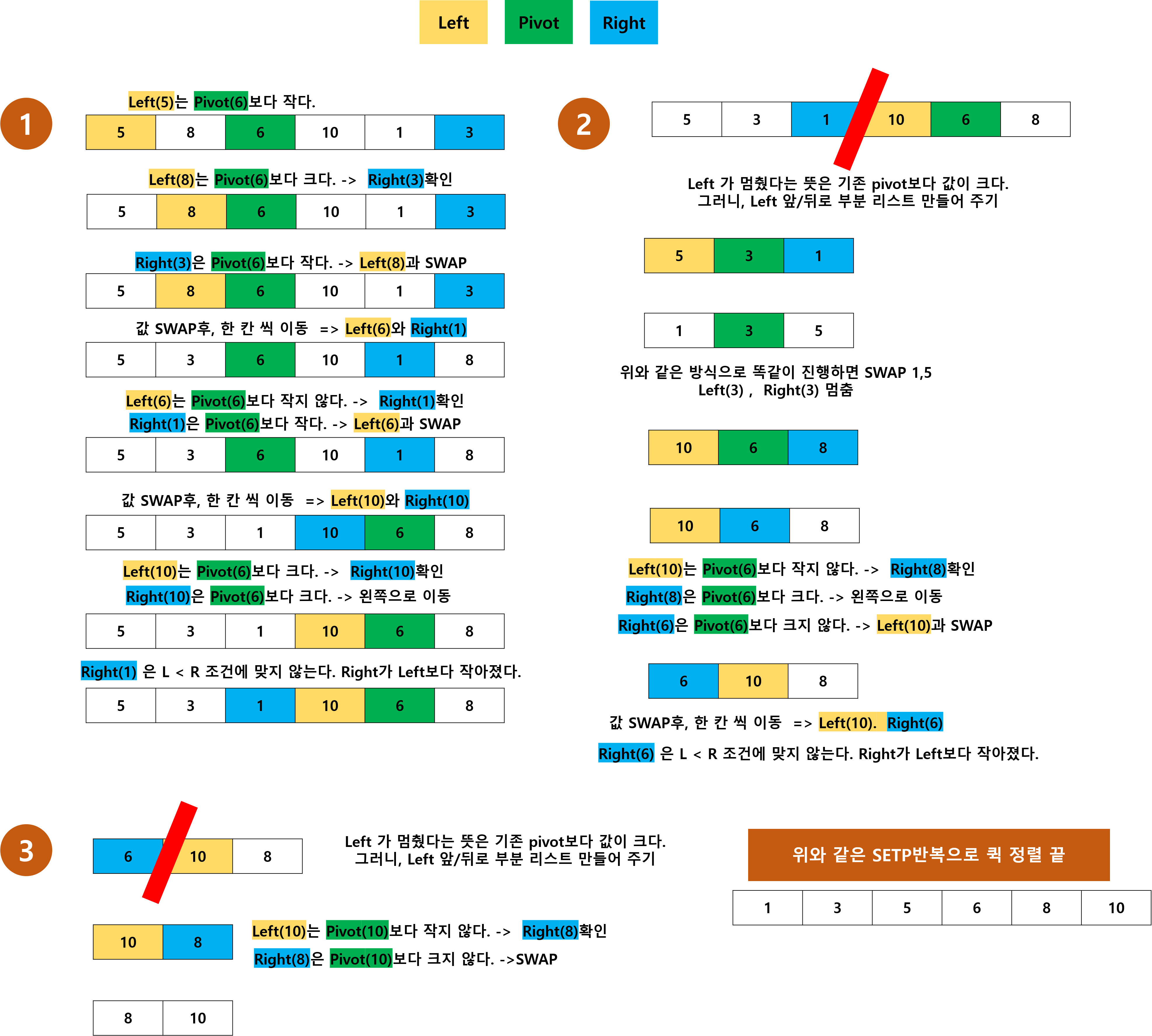
아래 예시를 통해 이해를 해보자.
Quick Sort (퀵 정렬) 의 장 · 단점
장점 :
- 속도가 가장 빠르다.
- 같은 시간복잡도를 가지는 다른 정렬 알고리즘과 비교해도 가장 빠르다.
- 추가 메모리 공간을 필요로 하지 않는다.
단점 :
- 정렬된 리스트의 경우 분할방식으로 인해 오히려 수행시간이 더 오래걸린다.
- pivot을 무엇으로 선택하냐에 따라 시간복잡도가 다르다. 그래서 median of three 방식이 존재한다.
Quick Sort (퀵 정렬) 의 시간복잡도
pivot을 기준으로 부분리스트로 나눠진다. 절반으로 나눠지는 것이 보장되지 않기 때문에 best와 worst case 가 존재한다.
최선의 경우 (Best)
- 나누어지는 부분 리스트마다 절반씩 분할되는 경우
- O(nlog₂n)
평균 (Avg)
- O(nlog₂n)
최악의 경우 (Worst)
- 나누어지는 부분 리스트마다 1개와 그 나머지 리스트로 분할되는 경우
- 정렬된 리스트를 가지고 퀵 정렬을 실행할 때
- O(n^2)
Quick Sort (퀵 정렬) JAVA 구현
public class QuickSort {
public static void main(String args[]) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int n = Integer.valueOf(br.readLine());
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = Integer.valueOf(br.readLine());
}
quickSort(arr, 0, n - 1);
for (int i = 0; i < n; i++) {
sb.append(arr[i] + "\n");
}
System.out.println(sb);
}
public static void quickSort(int[] arr, int left, int right) {
int pivot = arr[(left + right) / 2];
int l = left;
int r = right;
while (l <= r) {
while (arr[l] < pivot)
l++;
while (arr[r] > pivot)
r--;
if (l <= r) {
int temp = arr[l];
arr[l] = arr[r];
arr[r] = temp;
l++;
r--;
}
}
if (left < l - 1)
quickSort(arr, left, l - 1);
if (l < right)
quickSort(arr, l, right);
}
}윗 예시를 코드를 통해 똑같이 적용.
n = 6, array = [5, 8, 6, 10, 1, 3]
'Algorithm' 카테고리의 다른 글
| [SORT] Merge Sort (합병 정렬) (0) | 2021.08.15 |
|---|---|
| [SORT] Insertion Sort (삽입 정렬) (0) | 2021.07.26 |
| [SORT] Bubble Sort (버블 소트) (0) | 2021.07.26 |
| [SORT] Selection Sort (선택 정렬) (0) | 2021.07.26 |